Давайте несколько вещей из пути в первую очередь. Это не ваш регулярный Smashing Magazine статьи. Это не «как»; он не покажет вам, как построить лучшее меню или улучшить свой проект завтра. Эта статья показывает вам, как основная проблема в области компьютерных наук работает и почему мы все делая вид, что мы знаем что-то наверняка, когда мы действительно понятия не имею.
Вы смотрите на Smashing Magazine прямо сейчас, потому что вы стоите на плечах гигантского предположения под названием «P против NP». Это математическая проблема, которая защищает правительства, управляет Интернетом и делает возможным покупки в Интернете.
Возможно, вы никогда не слышали о P против NP, но эта статья будет ходить вам через него, показать вам, как она работает и объяснить, почему это имеет значение. Есть небольшая математика, но не волнуйтесь; это все довольно легко.
P против NP является математический вопрос под видом философского. Он описывает разницу между решением проблемы и зная, были ли вы решены ее. Начнем с простого примера, известного как «путешествия продавец» проблемы.
Наш продавец идет по городу с домами, разбросанными по нескольким улицам. Он должен посетить каждый дом один раз и только один раз. Продавец хочет найти самый быстрый маршрут, который ведет его в каждый дом, но требует как можно меньше ходить, как это возможно.

Продавец не знает, лучше ли начинать с верхнего правого, или идти к середине первым, или ходить по городу и начинать с другой стороны. Единственный способ, которым он может знать наверняка, это попробовать каждый маршрут и измерить, сколько времени это займет. Там нет формулы он может следовать, чтобы выяснить, самый быстрый маршрут; он должен найти ответ с грубой силой. Поиск ответа является «NP» часть, которую мы определим в ближайшее время.
Зная, нашел ли он ответ, легко. Если он посетил каждый дом, то он сделал работу; если он пропустил один, то он должен начать все сначала. Это часть «P». Все P против NP проблемы трудно решить, но легко проверить.
Да, есть некоторые большие слова
«P» в P против NP означает полиномиальное время. Это просто означает, что мы можем предсказать максимальное количество времени, которое потребуется для решения проблемы. Классическим примером полиномиального времени является быстрый сортировка. Вот набор блоков:
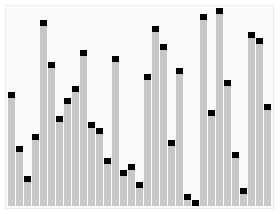
Мы хотим, чтобы сортировать их для того, чтобы быть самыми короткими до самыми высокими. Самый простой способ сделать это, разделив группу пополам, толкая высокие блоки вправо и короткие блоки влево. Затем мы разрезали каждую половину пополам и повторяли.
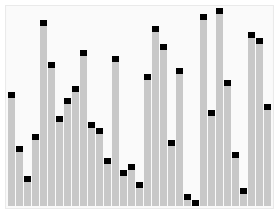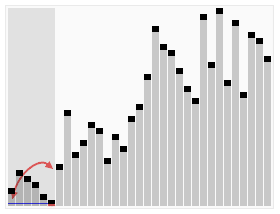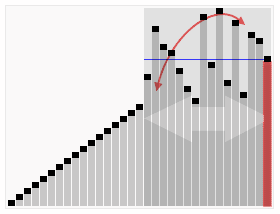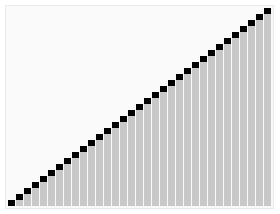
Есть алгоритм, который подскажет нам, сколько времени это займет. Не имеет значения, сколько блоков у нас есть или как дезорганизованы они, мы всегда можем предсказать наихудший сценарий, сколько времени потребуется, чтобы сортировать любое количество блоков. Предсказуемой частью является то, что делает его принимать только полиномиальное время. Все общие математике мы используем — добавление, алгебра, балансировка чековой книжки — может быть сделано в полиномиальное время.
NP означает недетерминированное полиномиальное время. Это в основном противоположность P: Там нет уравнения или формулы, чтобы предсказать, сколько времени потребуется, чтобы решить проблему. Как правило, единственный способ решить такого рода проблемы заключается в том, чтобы продолжать пытаться ответы, пока мы не найдем тот, который работает. Выяснение наилучшего маршрута для нашего продавца является NP-полной проблемой.
Давайте посмотрим на несколько маршрутов, которые мог бы пройти наш продавец. Он мог бы начать сверху и спуститься влево:
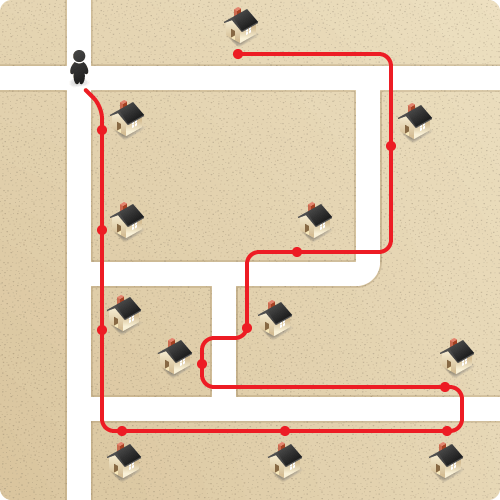
Это около 75 шагов. Он также может начать с ходьбы к середине и цикл вокруг против часовой стрелки:
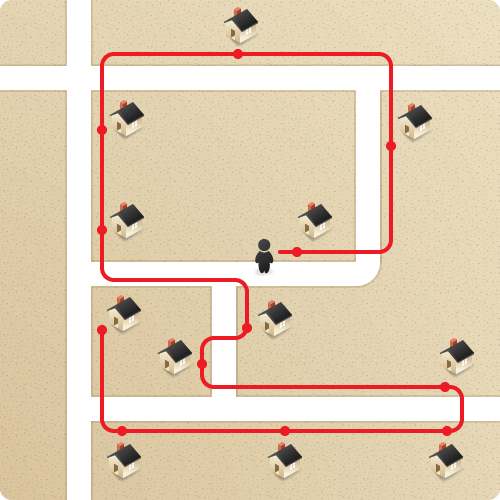
Это примерно 95 шагов. Продавец может также повернуть карту вокруг и начать с верхнего правого. Теперь он может избежать цикла все наоборот:
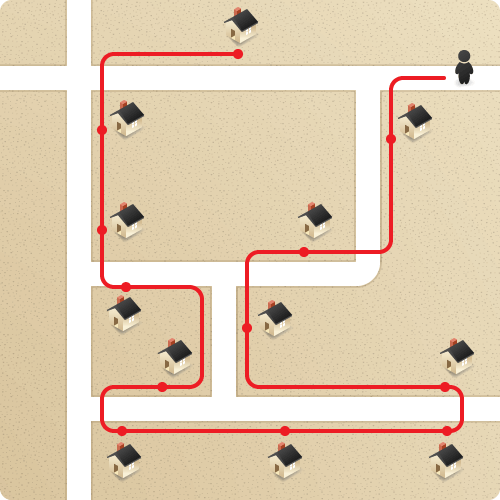
Этот маршрут около 80 шагов.
Хотя мы можем измерить каждый маршрут, чтобы увидеть, что является кратчайшим, нет никакого способа, чтобы сказать длины, не пытаясь их. Мы можем гадать, но довольно скоро мы просто должны начать ходить. Проблема коммивояжера известна, потому что посещение каждого дома по кратчайшей маршруту NP (очень трудно), но убедившись, чтобы посетить каждый дом P (очень легко).
Мы могли бы выяснить эту карту в течение нескольких минут, но добавление еще несколько домов сделает решение займет несколько часов. Добавить достаточно домов и решение займет годы.
Почему все это имеет значение
Коммивояжера является милой проблемой, но последствия гигантские.
Измените продавца на запрос страницы и дома на серверы, и у вас есть интернет-пакетная реуктора. Когда мой компьютер в Бостоне хочет отправить запросы на компьютер в Лондоне, он должен выяснить путь, чтобы туда добраться, подпрыгивая с одного сервера на другой по пути. Данные могут принимать тысячи различных маршрутов через тысячи различных компьютеров между Бостоном и Лондоном. Поиск самый быстрый маршрут является более крупной версией нашей проблемы продавца.
Google, Facebook и Apple пытаются упростить проблему, строя центры обработки данных вблизи крупных городов. Они пытаются сделать карту меньше, когда люди делают запросы.
Если бы вы могли выяснить лучший способ маршрутификатировать данные в Интернете, вы могли бы сделать биржевые торги быстрее, чем все остальные, и сделать миллиарды долларов.
Другая версия этой проблемы все о секретах.
Большая часть Интернета работает на секреты. Я хочу дать свой номер кредитной карты Amazon, но не парню, сидящему рядом со мной в Starbucks. Я не хочу делиться своим банковским паролем с моими соседями, и я не хочу, чтобы мои frenemies читать мою электронную почту. Вы можете делать покупки, делиться и работать в Интернете из-за секретов, и все эти секреты основаны на математике.
Большинство секретов в Интернете защищены криптографией с открытым ключом. Эта криптография основана на поиске двух больших чисел, которые, умноженные вместе, равны очень большому числу. 2 больших номера факторы очень большого номера. (Подумайте о рюкзаке, полном веса. Вы можете знать, что пакет весит 10 килограммов, но вы не знаете, имеет ли она один 10-килограммовый вес, 10 однокилограммовых весов или что-нибудь между ними.)
Возьмем, к примеру, число 26. Он имеет четыре фактора: 1, 2, 13 и 26. Каждое число содержит 1 и само число, поэтому мы будем игнорировать эти факторы; важные из них 2 и 13.
2 × 13 = 26Вы можете найти факторы 26, пытаясь каждый номер между 1 и 26. Это намного сложнее с mindbendingly большое число, как:
33478071698956898786044169848212690817704794983713768568912431388982883793878002287614711652531743087737814467999489
Можете ли вы найти факторы этого числа? Я дам тебе один ответ.
36746043666799590428244633799627952632279158164343087642676032283815739666И
511279233373417143396810270092798736308917Эти цифры головокружительно велики. Вы никогда не могли бы работать их на листе бумаги, и не может компьютер. Там нет хорошего способа написать компьютерную программу, чтобы найти факторы большого числа быстро. Лучшее, что вы можете сделать, это отказаться от чисел, которые явно не работают, а затем искать факторы один за одним среди триллионов и триллионов номеров, оставшихся. Поиск факторов является проблемой NP.
Мне пришлось потрудиться, чтобы найти эти факторы (ну, я посмотрел их на Википедии, но кто-то упорно трудился, чтобы найти их). Убедиться, что я прав, легко. Можно написать небольшую компьютерную программу для умножения второго и третьего чисел. Если они производят первый номер, то я прав, и они являются факторами. Ваша работа проста; это проблема P-уровня.
Если найти эти факторы было легко, то Интернет будет падать.
P Vs. NP
Наличие секрета не очень полезно, если я не могу доказать, что у меня есть, но я не могу просто сказать вам секрет, потому что тогда это не будет секретом. Мне нужно доказать, что я знаю ценность, не говоря вам, что это такое. Вот где факторы приходят дюйма Большепервое первое число доказывает, что я знаю факторы, даже не говорю вам, что эти цифры. Взгляните на «Рюкзак Алгоритмы и публично-ключевая криптография Made Easy«, если вы заинтересованы в том, как факторинг превращается в криптографию.
Если бы вы могли придумать способ быстро найти большие факторы, то вы могли бы украсть мои секреты. Роберт Редфорд снялся в фильме об этом.
Многие умные люди работают над тем, чтобы найти эти факторы, и они еще не нашли его. Мы основывали всю безопасность Интернета на «факт», что нет простого способа найти факторы большого числа, но это не факт. Мы не знаем, существует ли быстрый способ найти факторы или получить указания для нашего продавца. Может быть, это там, и мы просто не нашли его еще. Может быть, кто-то найдет его завтра. Это то, что P против NP это все о.
ПЗ НП
Сейчас мы предполагаем, что P не равна NP. Это означает, что некоторые проблемы легко, а другие трудно. Мы думаем, что наши секреты в безопасности, но мы не можем это доказать.
Математика основана на многих предположениях. Некоторые из этих предположений длятся десятилетия, прежде чем их докажут верными или ложными. До тех пор, пока предположение, что P не равно NP остается правдой, то мы можем сохранить обмен секретами, электронной почтой и номерами кредитных карт в Интернете без каких-либо проблем. Если вы доказали, что P делает равный NP, то вы можете вызвать некоторые большие неприятности.
P и NP
Некоторые люди делают философский аргумент, что P просто не может равняться NP. Если это так, то это будет означать, что найти решение проблемы всегда было так же просто, как проверка того, что решение является правильным и что факторинг наших больших чисел легко. Это нарушит всю криптографию в Интернете. SSL перестанет защищать что-либо, и вы никогда не сможете дать свою кредитную карту безопасно никому.
Это имеет еще большие последствия. Если P равняется NP, то вы можете решить что-нибудь так же легко, как вы могли бы проверить его. Любой, кто мог управлять автомобилем, мог построить ее, а любой, кто мог послушать симфонию, мог написать ее. Это делает мою голову больно, но это не реальная проблема.
Если бы вы могли создать практический пример P равный NP, то вы могли бы решить проблему коммивояжера и изменить весь способ, которым работает интернет-маркетинг. И это только начало.
Практическое решение, доказываюющее, что P равняется NP даст вам огромный контроль над информацией во всем мире.
Что будет дальше?
Базирование всего Интернета на предположение страшно. Мы хотим знать, является ли P равняется NP. Ответ имеет практическое применение, но он также задает большой вопрос о том, как мы выяснить вещи. Знаем ли мы их в первую очередь и понять их второй, или мы должны работать над решением, прежде чем мы сможем найти его?
Некоторые проблемы трудно, а некоторые просто смотреть трудно. P против NP дает нам основу, чтобы выяснить, что есть что.
Если вы можете доказать P против NP так или иначе, вы бы выиграть миллион долларов.
Источник: smashingmagazine.com